Let’s say you wish to measure the connection between a number of variables. One of many best methods to do that is with a linear regression (e.g., extraordinary least squares). Nonetheless, this system assumes that the connection between all variables is linear. One may additionally use generalized linear fashions (GLM) through which variables are reworked, however once more the connection between the result and the reworked variable is–you guessed it–linear. What if you happen to needed to mannequin the next relationship:
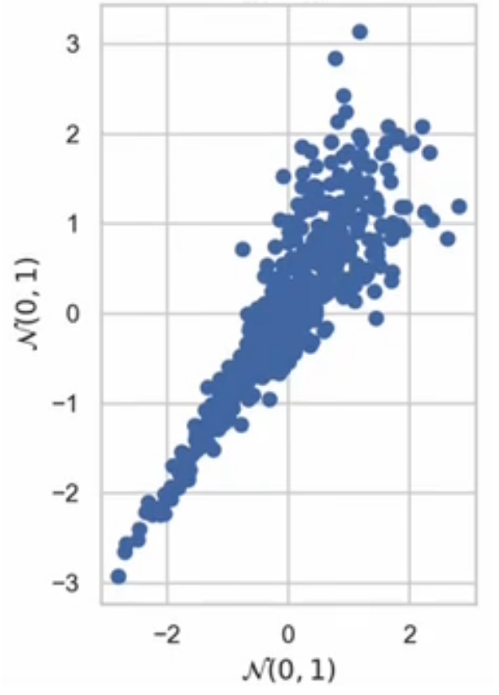
On this knowledge, each variables are usually distributed with imply of 0 and commonplace deviation of 1. Moreover, the connection is essentially co-monotonic (i.e., because the x variable will increase so does the y). But the correlation is just not fixed; the variables are intently correlated for small values, however weakly correlated for giant values.
Does this relationship truly exist in the actual world? Definitely so. In monetary markets, returns for 2 totally different shares could also be weakly constructive associated when shares or going up; nonetheless, throughout a monetary crash (e.g., COVID, dot-com bubble, mortgage disaster), all shares go down and thus the correlation could be very robust. Thus, having the dependence of various variables range by the values of a given variable is very helpful.
How may you mannequin any such dependence? A nice collection of movies by Kiran Karra explains how one can use copulas to estimate these extra complicated relationships. Largely, copulas are constructed utilizing Sklar’s theorem.
Sklar’s theorem states that any multivariate joint distribution will be written by way of univariate marginal distribution features and a copula which describes the dependence construction between the variables.
https://en.wikipedia.org/wiki/Copula_(probability_theory)
Copulas are fashionable in high-dimensional statistical functions as they permit one to simply mannequin and estimate the distribution of random vectors by estimating marginals and copulae individually.
Every variable of curiosity is reworked right into a variable with uniform distribution starting from 0 to 1. Within the Karra movies, the variables of curiosity are x and y and the uniform distributions are u and v. With Sklar’s theorem, you possibly can remodel these uniform distributions into any distribution of curiosity utilizing an inverse cumulative density perform (which might be the features F-inverse and G-inverse respectively.
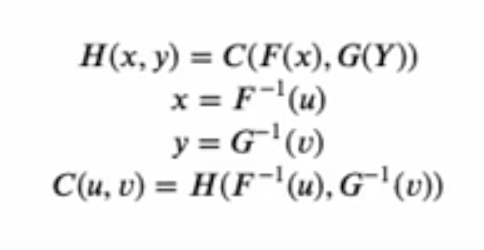
In essence, the 0 to 1 variables (u,v) serve to rank the values (i.e., percentiles). So if u=0.1, this offers the tenth percentile worth; if u=0.25, this offers the twenty fifth percentile worth. What the inverse CDF features do is say, if you happen to say u=0.25, the inverse CDF perform will provide you with the anticipated worth for x on the twenty fifth percentile. In brief, whereas the maths appears sophisticated, we’re actually simply in a position to make use of the marginal distributions primarily based on 0,1 ranked values. Extra data on the maths behind copulas is beneath.
The following query is, how will we estimate copulas with knowledge? There are two key steps for doing this. First, one wants to find out which copula to make use of, and second one should discover the parameter of the copula which most closely fits the info. Copulas in essence intention to search out the underlying relies upon construction–the place dependence is predicated on ranks–and the marginal distributions of the person variables.
To do that, you first remodel the variables of curiosity into ranks (principally, altering x,y into u,v within the instance above). Beneath is a straightforward instance the place steady variables are reworked into rank variables. To crease the u,v variables, one merely divides by the utmost rank + 1 to insure values are strictly between 0 and 1.

As soon as we now have the rank, we are able to estimate the connection utilizing Kendall’s Tau (aka Kendall’s rank correlation coefficient). Why would we wish to use Kendall’s Tau slightly than a daily correlation? The reason being, Kendall’s Tau measure the connection between ranks. Thus, Kendall’s Tau is equivalent for the unique and ranked knowledge (or conversely, equivalent for any inverse CDF used for the marginals conditional on a relationship between u and v). Conversely, the Pearson correlation might range between the unique and ranked knowledge.
Then one can decide a copulas type. Widespread copulas embrace the Gaussian, Clayton, Gumbel and Frank copulas.
The instance above was for 2 variables however one power of copulas is that can be utilized with a number of variables. Calculating joint chance distributions for a lot of variables is usually sophisticated. Thus, one method to attending to statistical inference with a number of variables is to make use of vine copulas. Vine copulas depend on chains (or vines) or conditional marginal distributions. In brief, one estimat
For example, within the 3 variable instance beneath, one estimates the joint distributions of variable 1 and variable 3; the joint distribution of variable 2 and variable 3 after which one can estimate the distribution of variable 1 conditional on variable 3 with variable 2 conditional on variable 3. Whereas this appears complicated, in essence, we’re doing a collection of pairwise joint distributions slightly than making an attempt to estimate joint distributions primarily based on 3 (or extra) variables concurrently.
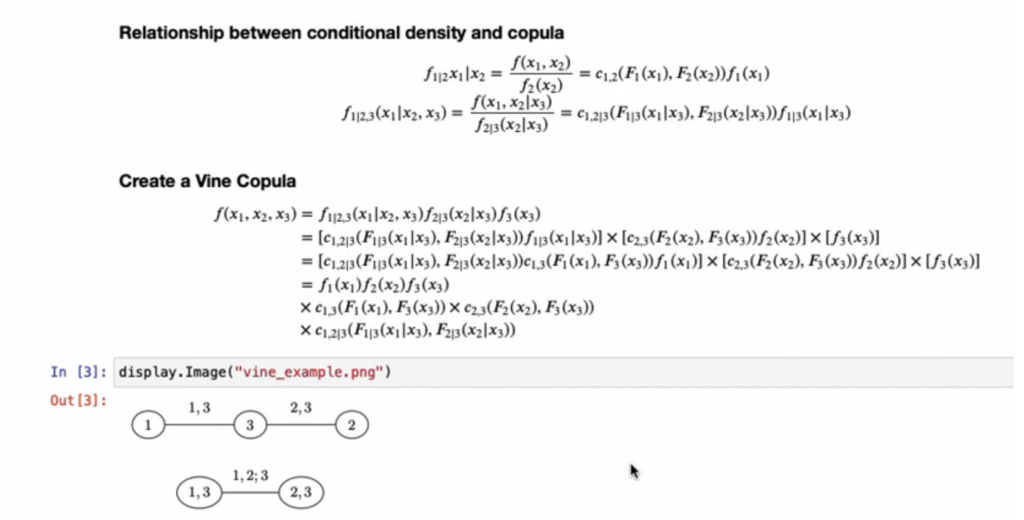
The video beneath describes vine copulas and the way they can be utilized for estimating relationships for greater than 2 variables utilizing copulas.
For extra element, I like to recommend watching the complete collection of movies.
